2020-03-11

BDD（Binary Decision Diagram）とは（直感的に）

BDD 論理函数機械学習

はじめに

この記事は，湊先生のpdf(BDD/ZDD を用いたグラフ列挙索引化技法，離散構造処理系: その概要と最近の研究状況について)，そしてKnuth先生のThe Art of Computer Programming Vol. 4, Fascicle 1などを参考にし，自分が理解できるように図を入れて書いています．

The Art of Computer Programming, Volume 4, Fascicle 1: Bitwise Tricks & Techniques; Binary Decision Diagrams by Donald E. Knuth(2009-03-27)

作者:Donald E. Knuth
メディア: 文庫

The Art of Computer Programming Volume 4, Fascicle 1 Bitwise Tricks & Techniques; Binary Decision Diagarms 日本語版 (ASCII Addison Wesley Programming Se)

作者:Donald E. Knuth
発売日: 2011/05/20
メディア: 大型本

この記事の流れ

まずは論理函数について軽く触れ，次にその論理函数を表す二分決定木について軽く説明をします．その後，簡単にBDDの直感的な説明をして終わりたいと思います．

厳密な内容については，大学の先生方に伺ってください．

論理函数

論理函数とは，簡単にいうといくつかの真理値をとり， $0$ または $1$ を返す函数のことです．本記事を通して，次のような論理函数を考えてみます．

$F(a, b, c) = (a \wedge \bar{b} \wedge c ) \vee (\bar{a} \wedge b \wedge \bar{c})$

この関数を真理値表で見ると，次のようになります．

$a$	$b$	$c$	$a \wedge \bar{b} \wedge \bar{c}$	$\bar{a} \wedge b \wedge \bar{c}$	$F(a, b, c)$
$0$	$0$	$0$	$0$	$0$	$0$
$0$	$0$	$1$	$0$	$0$	$0$
$0$	$1$	$0$	$0$	$1$	$1$
$0$	$1$	$1$	$0$	$0$	$0$
$1$	$0$	$0$	$1$	$0$	$1$
$1$	$0$	$1$	$0$	$0$	$0$
$1$	$1$	$0$	$0$	$0$	$0$
$1$	$1$	$1$	$0$	$0$	$0$

$a \wedge \bar{b} \wedge \bar{c} = 1$ もしくは $\bar{a} \wedge b \wedge \bar{c} = 1$ の所のみ $F(a, b, c) = 1$ となっていることがわかると思います．

二分決定木(Binary Decision Tree)

真理値表で見てもまだわかりにくいので，これを二分決定木で表現してみようと思います．具体的には，先ほどの $F(a, b, c)$ は次のように書けます．

f:id:OCELOT:20200309191937p:plain — 二分決定木

この木の根( $a$ のラベルがついているノード)から下に辿っていき， $1$ の葉に辿り着くような経路が $F(a, b, c) = 1$ となる組み合わせを表現しています．例えば $0 \to 1 \to 0$ と辿ると，これは $1$ の葉に辿り着き，かつ $F(a, b, c) = 1$ を満たします．

こう見ると，なんだかとてもわかりやすい気がしますね．

BDD (Binary Decision Diagram)

先ほどの二分決定木は，ノード数が指数的に増加してしまい，これを愚直に構築しようとすると領域計算量がとんでもないことになってしまいます．

そこで，次の二つの縮約規則を可能な限り適用することで二分決定木を圧縮します．

冗長な節点の削除
この規則は，今回の例では次のように書けます．
縮約規則１：冗長な節点の削除
この図だと，
「頂点 $c$ を経由しても行き着く先は $0$ なので，それならば $c$ は経由せずに直接 $0$ に行こう」
といった感覚でしょうか．
等価な節点の削除
この規則は，今回の例では次のように書けます．
縮約規則２：等価な節点の削除
この規則の気持ちを言うとすれば，
「同じことを何回も書くなら一個にまとめてしまおう」
という感じでしょうか．

どちらの規則も直感的で，すごくわかりやすいと思います．これらの規則を可能な限り適用すると，次のBDDが得られます．

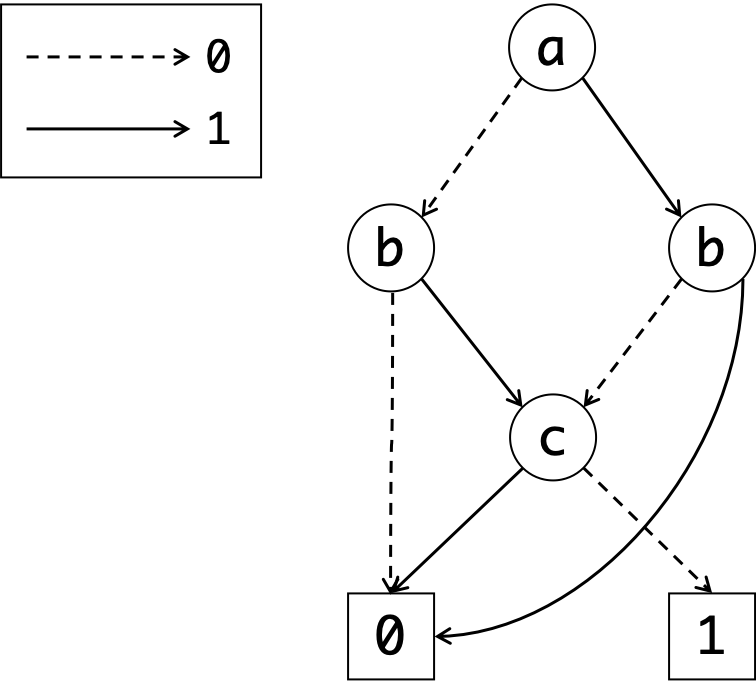
元の二分決定木に比べて非常にコンパクトにまとまりましたね．このようにしてBDDが得られるわけですが，規則の適用順番を変えると得られるBDDの形も変わるのではないか，という疑問が浮かびます．しかし，実際にはどのような順番で規則を適用しても，得られるBDDは一意に定まるそうです！

ただ，圧縮できると言っても，BDDを作るために二分決定木を構築してしまうのでは領域がもったいない気がします．でも安心してください，BDDは二分決定木を一旦構築することなく，直接構築できるという利点があるそうです！

このことについてはまたいつか書こうかと思います．

2020-03-05

僕のヒーローアカデミア（167話）：エクトプラズム先生の積分の問題

積分双曲線函数高校数学僕のヒーローアカデミア

僕のヒーローアカデミア第167話（18巻）の問題を解いてみようと思います．

僕のヒーローアカデミア 18 (ジャンプコミックス)

作者:堀越耕平
発売日: 2018/04/04
メディア: コミック

具体的には，次の定積分を計算する問題です．

$\displaystyle{ I := \int_{0}^{\ln (1+\sqrt{2})} \left( \frac{e^{x} - e^{-x}}{2} \right)^{3} \left( \frac{e^{x} + e^{-x}}{2} \right)^{11} \; dx }$

下図の水色の領域の面積を計算する問題ですね． f:id:OCELOT:20200305172130p:plain

双曲線函数

表記を簡単にするために，「双曲線函数」というものを導入します．双曲線函数とは指数関数 $e^{x}$ を用いて

$\displaystyle{ \sinh x = \frac{e^{x} - e^{-x}}{2} \\ \cosh x = \frac{e^{x} + e^{-x}}{2} \\ \tanh x = \frac{\sinh x}{\cosh x} }$

と定義されます．特に今回は $\sinh x$ （ハイパボリックサイン，hyperbolic sine）， $\cosh x$ （ハイパボリックコサイン，hyperbolic cosine）を使います． $\sinh x$ ， $\cosh x$ の性質として，次のものが知られています．

$\displaystyle{ \frac{d}{dx} \sinh x = \cosh x \\ \frac{d}{dx} \cosh x = \sinh x \\ \cosh^{2} x - \sinh^{2} x = 1 }$

ぜひ手を動かして確認してみてください．

また，微分の連鎖律から直ちに次の式も得られます．

$\displaystyle{ \frac{d}{dx} \sinh^n x = n \cdot \cosh x \cdot \sinh^{n-1} x \\ \frac{d}{dx} \cosh x = n \cdot \sinh x \cdot \cosh^{n-1} x }$

双曲線函数は面白い函数なので，詳しく知りたい方はWikipediaなどを参照してください．

解いてみる

まず，この定積分は $\sinh x$ と $\cosh x$ を使って次のように表せます．

$\displaystyle{ I = \int_{0}^{\ln (1+\sqrt{2})} \sinh^{3} x \cdot \cosh^{11} x \; dx }$

双曲線函数の関係式

$\displaystyle{ \cosh^{2} x - \sinh^{2} x = 1 }$

より，

$\displaystyle{ \begin{eqnarray} I &=& \int_{0}^{\ln (1+\sqrt{2})} \sinh x \cdot (\cosh^{2} x - 1)\cdot \cosh^{11} x \; dx \\ &=& \int_{0}^{\ln (1+\sqrt{2})} \sinh x \cdot \cosh^{13} x \; dx - \int_{0}^{\ln (1+\sqrt{2})} \sinh x \cdot \cosh^{11} x \; dx \\ &=& J - K \end{eqnarray} }$

と書けます．ただし，

$\displaystyle{ J = \int_{0}^{\ln (1+\sqrt{2})} \sinh x \cdot \cosh^{13} x \; dx \\ K = \int_{0}^{\ln (1+\sqrt{2})} \sinh x \cdot \cosh^{11} x \; dx }$

とおきました．これらをそれぞれ計算してみようと思います．

部分積分の公式と $J$ の定義から，

$\displaystyle{ \begin{eqnarray} J &=& \int_{0}^{\ln (1+\sqrt{2})} \sinh x \cdot \cosh^{13} x \; dx \\ &=& \left[ \cosh^{14} x\right]_{0}^{\ln (1+\sqrt{2})} - \int_{0}^{\ln (1+\sqrt{2})} \cosh x \cdot \left( 13\cdot \sinh x \cdot \cosh^{12} x\right) \; dx \\ &=& \left[ \cosh^{14} x\right]_{0}^{\ln (1+\sqrt{2})} - 13 \int_{0}^{\ln (1+\sqrt{2})} \sinh x \cdot \cosh^{13} x \; dx \\ &=& \left[ \cosh^{14} x\right]_{0}^{\ln (1+\sqrt{2})} - 13 J \end{eqnarray} }$

と変形できるので，

$\displaystyle{ J = \frac{1}{14} \left[ \cosh^{14} x\right]_{0}^{\ln (1+\sqrt{2})} }$

が得られます．同様の計算で， $K$ に関しても

$\displaystyle{ K = \frac{1}{12} \left[ \cosh^{12} x\right]_{0}^{\ln (1+\sqrt{2})} }$

という式が得られます．ここで，

$\displaystyle{ e^{\ln (1+\sqrt{2})} = 1 + \sqrt{2}, \quad e^{- \ln (1+\sqrt{2})} = \frac{1}{1 + \sqrt{2}} = - 1 + \sqrt{2} }$

より，

$\displaystyle{ \cosh \left( \ln (1 + \sqrt{2} ) \right) = \frac{e^{\ln (1+\sqrt{2})} + e^{- \ln (1+\sqrt{2})}}{2} = \sqrt{2} }$

と変形できるので，

$\displaystyle{ \begin{eqnarray} J & = & \frac{1}{14} \left[ \cosh^{14} x\right]_{0}^{\ln (1+\sqrt{2})} \\ & = & \frac{1}{14} \left( 2^7 - 1 \right) \\ K & = & \frac{1}{12} \left[ \cosh^{12} x\right]_{0}^{\ln (1+\sqrt{2})} \\ & = & \frac{1}{12} \left( 2^6 - 1 \right) \end{eqnarray} }$

となります．これらを $I = J - K$ に代入してあげれば，

$\displaystyle{ \begin{eqnarray} I &=& J - K \\ &=& \frac{1}{14} \left( 2^7 - 1 \right) -\frac{1}{12} \left( 2^6 - 1 \right) \\ &=& \frac{107}{28} \end{eqnarray} }$

が得られます．これは八百万さんの答えと同じですね！

僕のヒーローアカデミア 18 (ジャンプコミックス)

作者:堀越耕平
発売日: 2018/04/04
メディア: コミック

2020-03-02

Gurobi の使い方(C++)

最適化 Gurobi C++14

最適化ソルバの一つである Gurobi の使い方について．

はじめに
注意書き
環境構築
- 追記
ライセンスファイルの取得
コンパイル方法について
解きたい問題
プログラム
実行
終わりに

はじめに

これは私が頻繁に最適化ソルバを使うので，方法を忘れないための記事です．多少わかりにくいところ，もしくは使い方を間違っているところがあればぜひ教えてください．

注意書き

本記事を書いた時点で，私のダウンロードしている Gurobi のバージョンは 8.1.1. なので，この記事を参考にしてプログラムを書こうという方は適宜自分のバージョンに置き換えて読んでください．

環境構築

ダウンロード方法はこの記事を参考にすると良いと思います．

Macの場合，先ほどの記事などに従ってダウンロード後，解凍すると

/Library/gurobi811/mac64

というディレクトリができると思います． $GUROBI_HOMEなどの名前をつけておくと便利みたいです．

$ export GUROBI_HOME="/Library/gurobi811/mac64"

さて，C++の環境を構築するために以下を実行します．

$ cd $GUROBI_HOME/src/build
$ sudo make
$ sudo cp gurobi_c++.a $GUROBI_HOME/lib/

これで環境構築は終わりです．

追記

これコピーじゃなくてシンボリックリンクを貼れば十分です，すみません．つまり，最後の行は次の２行で書き換えてください．

$ cd $GUROBI_HOME/lib
$ ln -sf ./../src/build/libgurobi_c++.a libgurobi_c++.a

さらに，ubuntuの場合は次の行を ~/.bashrc に追記しましょう．

export LD_LIBRARY_PATH=$LD_LIBRARY_PATH:$GUROBI_HOME/lib

ちなみにpythonは

$ cd $GUROBI_HOME
$ python setup.py install

で環境構築完了だったと思います．

↓2020/05/02追記

ライセンスファイルの取得

まず，gurobiの公式サイトにアクセスし，ライセンスを取得します．
ライセンスを取得すると，下の方にgrbgetkey XXXXXXXX-XXXX-XXXX-XXXX-XXXXXXXXXXXXを実行してください（XXXXXXXX-XXXX-XXXX-XXXX-XXXXXXXXXXXXは英数字）と書いてあるので実行してみます．しかし，実際コマンドを打つとcommand not foundとなってしまいます．これは次のように対処すればいいです．

$ cd $GUROBI_HOME/bin
$ ./grbgetkey XXXXXXXX-XXXX-XXXX-XXXX-XXXXXXXXXXXX

しばらくすると，ライセンスファイルを置く場所を聞かれるので，置きたい場所を選んでください．これでライセンスファイルの取得は完了です．

コンパイル方法について

外部ライブラリを使う C++のコードはコンパイル時にたくさんのオプションを書かなければなりません．しかし，毎回書くのは大変なので，Makefileを作っておくと良いでしょう．今回の場合は，例えば次のようなMakefileを作れば良いと思います．

CCC = g++ -std=c++14
GUROBI = /Library/gurobi811/mac64
INCLUDE = $(GUROBI)/include
LIBRARY = $(GUROBI)/lib -lgurobi_c++ -lgurobi81

all: exec
  ./exec
exec: main.cpp
  $(CCC) -o exec main.cpp -I$(INCLUDE) -L$(LIBRARY)

これさえ作っておけば，コンパイル→実行は

$ make

だけなので楽チンですね．

解きたい問題

次式で定義される行列 $A \in \mathbb{R}^{2 \times 2}$ ，ベクトル $b \in \mathbb{R}^{2}$

$A = \begin{pmatrix} -1 & 2 \\ 0 & 1 \\ \end{pmatrix}, \quad b = \begin{pmatrix} 0 \\ 6 \end{pmatrix}$

を用いて，次のような最適化問題を考えます．

$\min \left\{ (x_{1} - 3)^2 + (x_{2} - 4)^2 \mid A x \leq b, x_{1} \geq 0, x_{2} \geq 0 \right\}$

この問題の最適値は $5$ で，最適解は

$x = \begin{pmatrix} x_{1} \\ x_{2} \end{pmatrix} = \begin{pmatrix} 4 \\ 2 \end{pmatrix}$

です．これらを求めるプログラムを書いてみようと思います．

プログラム

例えば，次のように書けます．

#include <iostream>
#include <gurobi_c++.h>

int main() {
    // 環境の宣言
    GRBEnv   env   = GRBEnv();
    // モデルの宣言
    GRBModel model = GRBModel( env );
    // 変数の宣言
    GRBVar   x1, x2;

    // 制約式の追加
    // 線形の式 → GRBLinExpr
    // 二次の式 → GRBQuadExpr
    GRBLinExpr  constraint_1 = 0.0; // -x + 2y <= 0 の制約式の左辺を格納する変数
    GRBLinExpr  constraint_2 = 0.0; // x       <= 6 の制約式の左辺を格納する変数
    GRBQuadExpr objective_function;  // 目的関数 x^2 + y^2 の式を格納する変数

    model.set( GRB_IntParam_OutputFlag, 0 ); // コンソールへの出力をなくす
    
    // 変数をモデルに追加
    //                 下界,         上界,  初期値,  変数の型（今回は連続値)
    x1 = model.addVar( 0.0, GRB_INFINITY,   0.0,   GRB_CONTINUOUS );
    x2 = model.addVar( 0.0, GRB_INFINITY,   0.0,   GRB_CONTINUOUS );
    model.update(); // モデルの更新

    // 制約式の追加
    constraint_1 = - x1 + 2*x2;
    model.addConstr( constraint_1 <= 0 );

    constraint_2 = x1;
    model.addConstr( constraint_2 <= 6 );
    model.update(); // モデルの更新

    // 目的関数の設定
    objective_function = (x1 - 3) * (x1 - 3) + (x2 - 4) * (x2 - 4);
    model.setObjective( objective_function, GRB_MINIMIZE );
    model.update(); // モデルの更新

    // ソルバに解いてもらう
    model.optimize();

    // 最適値の出力
    std::cout << "Optimal Value : " << model.get( GRB_DoubleAttr_ObjVal ) << '\n';

    // 最適解の出力
    std::cout << "Optimal Solution\n"
              << "\t x1 = " << x1.get( GRB_DoubleAttr_X ) << '\n'
              << "\t x2 = " << x2.get( GRB_DoubleAttr_X ) << std::endl;

    return 0;
}

解きたい問題が最大化問題である場合，model.setObjective( objective_function, GRB_MAXIMIZE ); と書きます．また，今回は制約が2つ（ $A$ の行数が2）だったので制約をconstraint_1, constraint_2のように別々に宣言しましたが，制約がたくさんある場合は

#include <vector>
size_t number_of_constraints;
std::vector< GRBLinExpr > constraints( number_of_constraints, 0.0 );

のように，std::vector型で宣言すると良いかもしれません．

実行

先ほどのプログラムをmain.cppという名前で保存し，同じディレクトリ内にMakefileも用意します．あとは，makeコマンドで結果が得られます．

$ make
g++ -std=c++14 -o exec main.cpp -I/Library/gurobi811/mac64/include -L/Library/gurobi811/mac64/lib -lgurobi_c++ -lgurobi81
./exec
Academic license - for non-commercial use only
Optimal Value : 5
Optimal Solution
     x1 = 4
     x2 = 2

応用すれば様々な問題が解けるので楽しいですね！

終わりに

最適化ソルバの使い方は公式サイトに書いてあります．しかし，英語の記事を読むのは私にとって大変ですのでもっと日本語の記事が欲しいなあと思っています．．

学習理論の学習

統計的学習理論を学習してるときに思ったこととか

BDD（Binary Decision Diagram）とは（直感的に）

はじめに

この記事の流れ

論理函数

二分決定木(Binary Decision Tree)

BDD (Binary Decision Diagram)

僕のヒーローアカデミア（167話）：エクトプラズム先生の積分の問題

双曲線函数

解いてみる

Gurobi の使い方(C++)

はじめに

注意書き

環境構築

追記

ライセンスファイルの取得

コンパイル方法について

解きたい問題

プログラム

実行

終わりに

$a$	$b$	$c$	$a \wedge \bar{b} \wedge \bar{c}$	$\bar{a} \wedge b \wedge \bar{c}$	$F(a, b, c)$
$0$	$0$	$0$	$0$	$0$	$0$
$0$	$0$	$1$	$0$	$0$	$0$
$0$	$1$	$0$	$0$	$1$	$1$
$0$	$1$	$1$	$0$	$0$	$0$
$1$	$0$	$0$	$1$	$0$	$1$
$1$	$0$	$1$	$0$	$0$	$0$
$1$	$1$	$0$	$0$	$0$	$0$
$1$	$1$	$1$	$0$	$0$	$0$

$a$	$b$	$c$	$a \wedge \bar{b} \wedge \bar{c}$	$\bar{a} \wedge b \wedge \bar{c}$	$F(a, b, c)$
$0$	$0$	$0$	$0$	$0$	$0$
$0$	$0$	$1$	$0$	$0$	$0$
$0$	$1$	$0$	$0$	$1$	$1$
$0$	$1$	$1$	$0$	$0$	$0$
$1$	$0$	$0$	$1$	$0$	$1$
$1$	$0$	$1$	$0$	$0$	$0$
$1$	$1$	$0$	$0$	$0$	$0$
$1$	$1$	$1$	$0$	$0$	$0$

$a$	$b$	$c$	$a \wedge \bar{b} \wedge \bar{c}$	$\bar{a} \wedge b \wedge \bar{c}$	$F(a, b, c)$
$0$	$0$	$0$	$0$	$0$	$0$
$0$	$0$	$1$	$0$	$0$	$0$
$0$	$1$	$0$	$0$	$1$	$1$
$0$	$1$	$1$	$0$	$0$	$0$
$1$	$0$	$0$	$1$	$0$	$1$
$1$	$0$	$1$	$0$	$0$	$0$
$1$	$1$	$0$	$0$	$0$	$0$
$1$	$1$	$1$	$0$	$0$	$0$