BDD（Binary Decision Diagram）とは（直感的に）

はじめに

この記事は，湊先生のpdf(BDD/ZDD を用いたグラフ列挙索引化技法， 離散構造処理系: その概要と最近の研究状況について)， そしてKnuth先生のThe Art of Computer Programming Vol. 4, Fascicle 1などを参考にし， 自分が理解できるように図を入れて書いています．

The Art of Computer Programming, Volume 4, Fascicle 1: Bitwise Tricks & Techniques; Binary Decision Diagrams by Donald E. Knuth(2009-03-27)

The Art of Computer Programming Volume 4, Fascicle 1 Bitwise Tricks & Techniques; Binary Decision Diagarms 日本語版 (ASCII Addison Wesley Programming Se)

この記事の流れ

まずは論理函数について軽く触れ， 次にその論理函数を表す二分決定木について軽く説明をします． その後，簡単にBDDの直感的な説明をして終わりたいと思います．

厳密な内容については，大学の先生方に伺ってください．

論理函数

論理函数とは，簡単にいうといくつかの真理値をとり， または を返す函数のことです． 本記事を通して，次のような論理函数を考えてみます．

この関数を真理値表で見ると，次のようになります．

もしくは の所のみ となっていることがわかると思います．

二分決定木(Binary Decision Tree)

真理値表で見てもまだわかりにくいので，これを二分決定木で表現してみようと思います． 具体的には，先ほどの は次のように書けます．

二分決定木

この木の根( のラベルがついているノード)から下に辿っていき， の葉に辿り着くような経路が となる組み合わせを表現しています． 例えば と辿ると，これは の葉に辿り着き，かつ を満たします．

こう見ると，なんだかとてもわかりやすい気がしますね．

BDD (Binary Decision Diagram)

先ほどの二分決定木は，ノード数が指数的に増加してしまい， これを愚直に構築しようとすると領域計算量がとんでもないことになってしまいます．

そこで，次の二つの縮約規則を可能な限り適用することで二分決定木を圧縮します．

• 冗長な節点の削除
  この規則は，今回の例では次のように書けます．

  

  縮約規則１：冗長な節点の削除

  この図だと，
  「頂点 を経由しても行き着く先は なので，それならば は経由せずに直接 に行こう」
  といった感覚でしょうか．
• 等価な節点の削除
  この規則は，今回の例では次のように書けます．

  

  縮約規則２：等価な節点の削除

  この規則の気持ちを言うとすれば，
  「同じことを何回も書くなら一個にまとめてしまおう」
  という感じでしょうか．

どちらの規則も直感的で，すごくわかりやすいと思います． これらの規則を可能な限り適用すると，次のBDDが得られます．

BDD

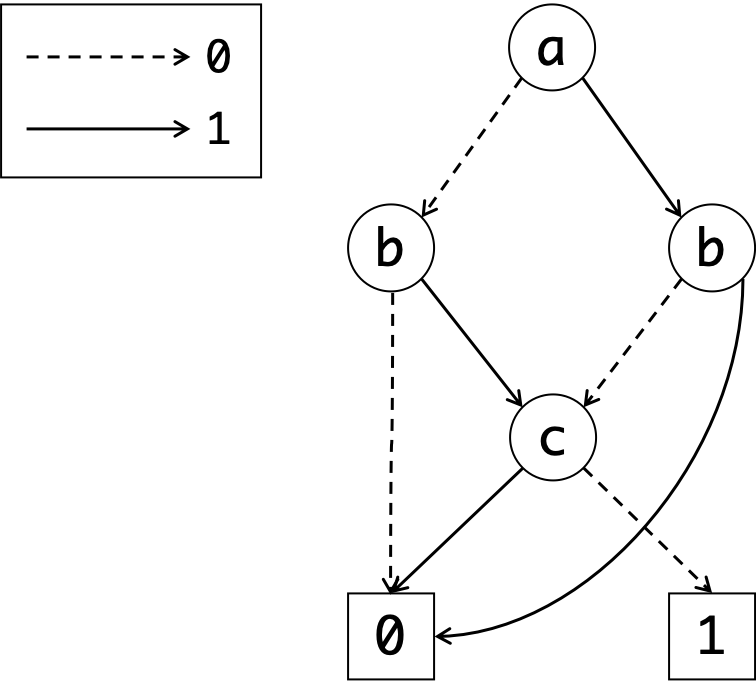
元の二分決定木に比べて非常にコンパクトにまとまりましたね． このようにしてBDDが得られるわけですが，規則の適用順番を変えると得られるBDDの形も変わるのではないか，という疑問が浮かびます． しかし，実際にはどのような順番で規則を適用しても，得られるBDDは一意に定まるそうです！

ただ，圧縮できると言っても，BDDを作るために二分決定木を構築してしまうのでは領域がもったいない気がします． でも安心してください，BDDは二分決定木を一旦構築することなく，直接構築できるという利点があるそうです！

このことについてはまたいつか書こうかと思います．